Often in clinical research, studies are conducted at a smaller scale than would be advisable to meet their statistical targets. This could be due to limited budgets, rarity of the condition studied, or focusing on a relatively small segment of the population (e.g., pediatrics). In recognition of these objective difficulties, the regulatory authorities may, on occasion, allow the supplementation of Synthetic Control Arms (SCA) with data from external, previously conducted studies. Other situations may include a scenario where a drug manufacturer wishes to compare an already-approved drug to its market competitors, but direct head-to-head comparison in a clinical trial is infeasible.
In this blog post we will cover SCA analysis and information borrowing from historical studies.
Synthetic Control Arm (SCA) Analysis
A synthetic control arm, often referred to as an external control arm, is a cohort of patients who did not receive the treatment studied and did not participate in the original clinical trial. The use of SCA is typically used to assess the efficacy of a new treatment that has only been tried in a single arm trial. By bringing in an SCA, the idea is to estimate comparative treatment or safety effects with as little bias as possible.
The data used for an SCA may be extracted from an external repository such as other clinical trials, an insurance claims database or an academic, prospective study. Integrating the trial and the external control arm will normally require a lengthy data harmonization process: retrospective application of the inclusion/exclusion criteria to rule out external control patients that would not be eligible to participate in a hypothetical trial. Even after harmonization, the two arms may still be rather imbalanced in terms of their covariate distribution: this may be crucial, if some covariates are informative of both the patient tendency to receive the treatment and the eventual outcome, i.e., confounders.
The most common class of covariate balancing methods are based on the propensity score (PS), which is the probability of receiving the treatment given the set of confounders. The PS is estimated from the data assuming no unobserved confounders and is therefore associated with a lot of uncertainty. PS methods include matching (matching controls to treated patients who “resemble” them the most) and weighting (assigning control patients fractional weights). An example of the distribution of a potential confounder (in this case “age”) in the two treatment groups, before and after the application of propensity score-based methods, is provided in Figure 1. Clearly, patients in the external control group tended to be younger than those in the treatment group. After assigning them weights (or alternatively, selecting a subset of them that resembles the treatment group more closely), the age profile of treated patients no longer differs considerably to that of the controls, and differences in their outcome cannot be attributed to differences in age.
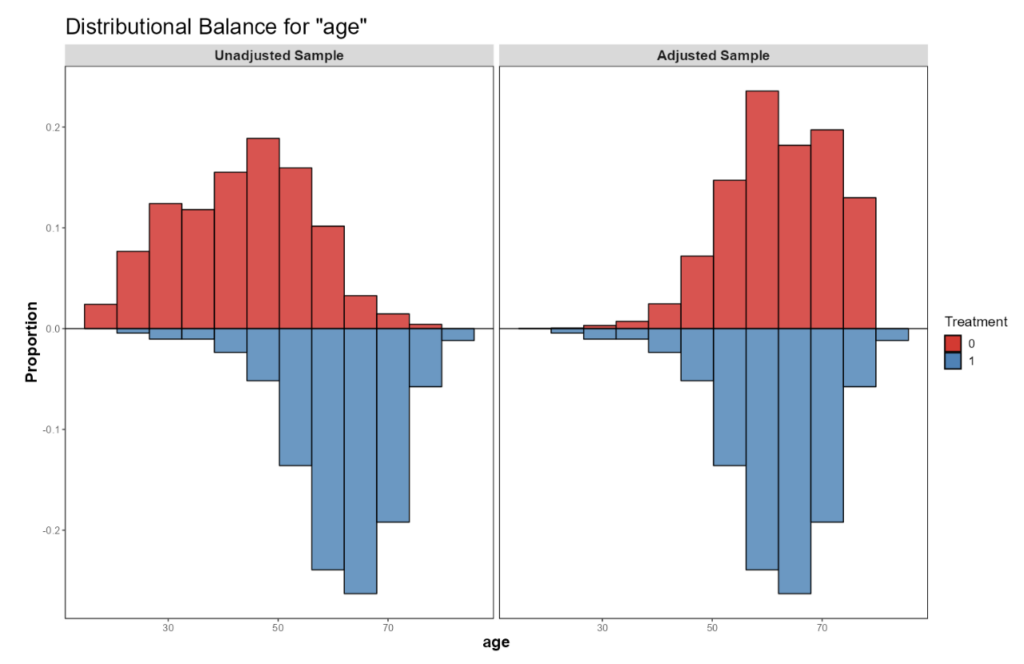
Figure 1: Age distribution in the treated and the external control groups before (left panel) and after applying propensity score-based methods. Sample balance after PS weighting or matching is typically assessed visually through inspection of the covariate distributions, as well as quantitatively using standardized mean differences (SMDs). What follows is estimation of the treatment effect using standard modelling techniques and the estimated weights, when applicable. Uncertainty in the results is now associated with patient-to-patient variability, PS estimation error, and outcome model lack-of-fit. To overcome these uncertainties, we may use bootstrapping or robust standard errors. The above does not address potential unmeasured confounding, whose impact is assessed via a set of techniques known as quantitative bias assessment (QBA).
Employing Bayesian principles, the historical studies in use induce a posterior distribution on relevant parameters. This posterior distribution may serve as a prior distribution for the clinical trial data, but this would be akin to pooling the historical studies with our current data. To address the fact that these are separate studies conducted in different patient population and in different time periods, we assign each historical study with a fractional number that reflects the proportion of a patient that each of their subjects contributes. This fraction takes the mathematical form of a power parameter, and the resultant prior distribution is subsequently called the power prior (Ibrahim & Chen, 2000). When the power parameters in the power prior model are estimated from the data and reflect the amount of commensurability between the historical and the current data, we call it dynamic borrowing (Viele et al., 2014).
Borrowing Information from Historical Studies Using The Power Prior Model
Another common way of synthesizing several data sources is by postulating a hierarchical Bayesian model (HBM). At the top hierarchy, we model the dependence of the observed outcome on the parameters of interest, and at the lower hierarchy we model the joint distribution of said parameters. The more diffuse the latter distribution is, the more heterogeneous the different studies are, and the less we can borrow from each to infer on the others. This variability is estimated from the data and can in fact be related to an equivalent power prior model (Chen & Ibrahim, 2006; Harari et al., 2023). These models are also popular in the analysis of basket trials, where cancer patients with different indications receive the same treatment and we believe that the response rates in the different subgroups may be informative of the response rates in other groups.
Hierarchical Bayesian Modelling Example: Systemic Lupus Erythematosus in Pediatric Patients (NCT01649765)
GSK and HGS (2012-2018) trialed their drug Benlysta® (Belimumab) in patients aged 12-17 with systemic lupus erythematosus (SLE). This trial followed two successful adult trials, and the primary efficacy outcome was the SLE Responder Index (SRI) response rate.
As a standalone trial, the pediatric trial would require ~800 children to achieve its goals: in reality, recruiting 100 patients would be a tall order. When designing a trial with borrowing information from the two historical trials, it can be shown (Harari et al., 2023) that if drug efficacy is established when the posterior probability of efficacy exceeds 97.5%, and borrowing is limited to no more than 26% of the information from either adult study, then 100 patients should suffice.
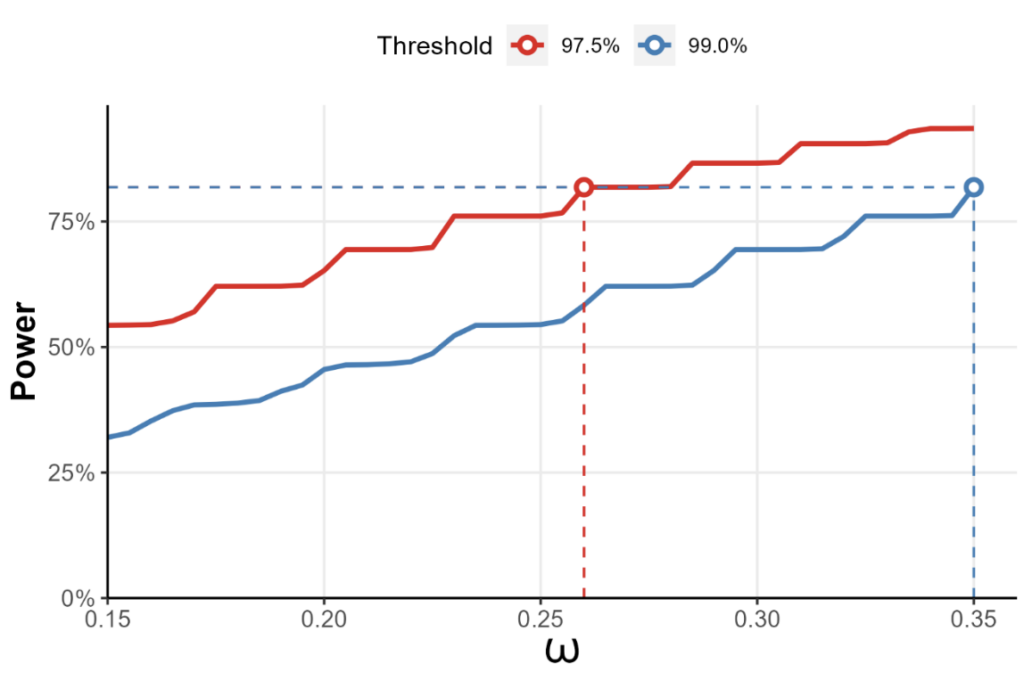
Figure 2: The statistical power of a test for treatment efficacy in the NCT01649765 trial, where the two adult trials form an evidence based for the pediatric trial to borrow information from. The x-axis represents the maximum fraction of the information allowed to be borrowed from either study. Here, if efficacy is established whenever the posterior probability of efficacy threshold exceeds 97.5%, borrowing no more than 26% from either study gives us 80% power, provided that we recruit 50 pediatric patients for either arm.
SLE in Pediatric Patients Example
The eventual trial included 93 pediatric patients. The results of the two adult trials and the eventual pediatric trial were as follows:

At the preset borrowing fraction of 26%, the posterior probability of drug efficacy can be shown to be 98.85%, well above the 97.5% threshold. The FDA approved Belimumab for children aged 5-17 based on a slightly different analysis but with a similar reasoning (US Food and Drug Administration, 2018).
Conclusion
The incorporation of Synthetic Control Arms (SCA) and information borrowing from historical studies represents a pivotal advancement in clinical trial design. Meticulous data harmonization, coupled with the use of covariate balancing methods – facilitated by lengthy discussions with domain experts and carefully drawing a directed acyclic graph (DAG) – can get us nearer emulating a randomized controlled trial. Techniques such as bootstrapping and robust standard errors further enhance result reliability. Additionally, quantitative bias assessment (QBA) provides a comprehensive evaluation of potential unmeasured confounding.
Furthermore, Bayesian principles offer powerful tools for synthesizing data from historical studies. The Power Prior Model, dynamic borrowing, and Hierarchical Bayesian Modelling may help tie together treatment effects across diverse patient populations and timeframes. Real-world examples, such as the Benlysta® trial in pediatric patients with Systemic Lupus Erythematosus, vividly illustrate the transformative potential of these approaches.
By embracing these innovative methodologies, researchers can navigate the complexities of clinical research, optimize study outcomes, and ultimately accelerate medical advancements.



